Spuneam în episodul anterior că atunci când materia dispare, când timpul dispare, rămâne geometria. Să înțelegem această afirmație care presupune că trebuie să vorbim despre diversele geometrii care pot coexista într-un spațiu Euclidian 3-dimensional. Care geometrii pot să fie explicate cel puțin intuitiv la nivelul de înțelegere al profanului doritor de cunoaștere, dar care ne dau șansa să înțelegem fizica universului dacă le-am privi prin limbajul geometriei diferențiale găsit de Gauss și abstractizat de Riemann.

I. De la relativitatea restrânsă la geometriile clasice

În absența timpului geometria cu patru dimensiuni a spațiu-timpului Minkowskian, care este un exemplu de univers fără materie – universul relativității restrânse – se reduce la o geometrie Euclidiană tridimensională. 

Asta pentru că dacă eliminăm coordonata temporală a acestui spațiu-timp, ceea ce rămâne este o teoremă 3-dimensională a lui Pitagora scrisă prin intermediul metricii, iar asta va face ca suprafețele din spațiul 3-dimensional rămas să se „încarce” cu geometrii proprii. 

Cel „vinovat” de această viziune a fost Carl Friedrich Gauss despre care am vorbit. Geometria lui diferențială scrisă conform coordonatelor suprafețelor conduce la așa ceva.

Geometria Euclidiană va fi geometria curburii constante 0 în plane, geometria neeuclidiană va fi geometria curburii constante negative obținută pe pseudosferă iar geometria sferică va fi geometria curburii constante pozitive obținută pe sfere. 

Orice altă suprafață prin coordonatele sale va avea o geometrie descriptibilă diferențial. Iar abstractizări în dimensiuni superioare sau pentru alte „spații-structuri geometrice” se datorează lui Riemann. 

II. Cazul geometriei Euclidiene plane

Cel mai simplu de înțeles ar fi că geometria euclidiană tridimensională, la nivelul fiecărui plan, produce geometria plană clasică — adică acea geometrie a lui Euclid, formulată în jurul anului 300 î.Hr., și reconfigurată axiomatic de David Hilbert în preajma anului 1900. Explicație: dacă eliminăm o dimensiune spațială, teorema lui Pitagora în trei dimensiuni se reduce la teorema lui Pitagora în două dimensiuni.

III. De la geometria Euclidiană plană la geometria neeuclidiană

Douăzeci și două de secole s-au scurs între cele două momente amintite anterior, iar cheia tuturor întrebărilor în această perioadă a fost legată de înțelegerea celebrului postulat al paralelelor.

Acest postulat afirmă: printr-un punct exterior unei drepte se poate duce o singură paralelă la acea dreaptă. Este o afirmație nedemonstrabilă, un dat, o regulă a jocului — și tocmai de aceea se numește postulat.

Consecința cea mai importantă? Faptul că suma unghiurilor oricărui triunghi este de 180°.

Ca să clarificăm tipul unității de măsură — nu ne referim, firește, la grade Celsius. Dacă luăm un segment OD, ținem punctul O fix și rotim segmentul complet în plan în jurul lui O, ajungem din nou în poziția inițială. Spunem atunci că am generat un unghi de 360°. Așadar, un unghi de 180° corespunde poziției simetrice față de direcția inițială.

Dar de unde știm că acest postulat este „dat”?  

Ei bine, dacă presupunem contrariul, adică dacă presupunem că printr-un punct exterior unei drepte pot trece mai multe paralele, obținem o geometrie consistentă, dar cu totul diferită: o geometrie în care suma unghiurilor unui triunghi este strict mai mică decât 180°. Aceasta este ceea ce numim geometrie neeuclidiană.

Și acum vine partea fascinantă: o astfel de geometrie poate fi modelată concret în spațiul nostru Euclidian 3-dimensional. Există o suprafață numită pseudosferă, cunoscută și ca suprafața Beltrami, după Eugenio Beltrami, cel care a demonstrat în mod constructiv existența sa. Pe această suprafață se poate arăta că un triunghi are întotdeauna suma unghiurilor mai mică decât 180°. În cazul limbajului matematic evoluat al geometriei diferențiale este simplu, prin acea teorema a lui Gauss care lega curbura suprafeței, aici constantă negativă, de suma unghiurilor unui triunghi construit pe ea. Așadar, geometria Euclidiană tridimensională generează pe suprafața pseudosferei o geometrie complet diferită de cea Euclidiană. Acesta a fost punctul de vedere prin geometrie diferențială.

Există însă și un alt mod de a explica de ce geometria pseudosferei este cea neeuclidiană.  Aici intervine acea forță specifică a matematicii: puterea de a analiza structuri și relațiile dintre structuri. Tocmai aceste relații între structuri oferă explicația profundă.

Iar cel care a avut viziunea transferului de structuri în acest caz, cel care a înțeles în profunzime felul în care o geometrie neeuclidiană odată evidențiată se poate vedea în altă formă echivalentă— a fost Henri Poincaré, unul dintre cei cinci giganți pe care eu îi numesc absolutul în matematică.

IV. Cazul geometriei sferice

Înainte de a intra în detaliile geometriilor neeuclidiene, să facem o observație esențială și mai ușor de înțeles: geometria Euclidiană tridimensională poate modela, pe suprafața unei sfere, o altă geometrie — și anume geometria sferică, o geometrie de tip eliptic. O geometrie de curbură constantă pozitivă.

În această lume geometrică, „dreptele” sunt cercuri mari ale sferei  — precum ecuatorul sau meridianele — iar suma unghiurilor unui triunghi sferic este strict mai mare decât 180°. Aceste fapte se pot demonstra chiar și elevilor de liceu.

Să explicăm intuitiv de ce un meridian de exemplu este „dreaptă” în această geometrie. Ne vom baza pe faptul că dreapta este drumul cel mai scurt care unește două puncte. 

Să ne închipuim sfera stând pe un plan ca o minge pe o masă. De la polul Nord N al sferei la polul Sud S vopsim meridianul cu roșu și rotim sfera până când tot meridianul este ștampilat pe planul tangent în S. Ceea ce se obține este un segment NS în acel plan. O altă curbă pe sferă care unește N cu S, ștampilată în plan prin rotiri și înclinări ale sferei produce o curbă NS în plan mai lungă decât segmentul NS obținut din ștampilarea meridianului. Deci meridianul va fi „dreaptă” pentru că produce segmentul de cea mai mică lungime în plan. De fapt orice cerc care se obține prin intersecția sferei cu un plan care trece prin centrul ei va fi „dreapta” a sferei, adică se va comporta prin ștampilare ca meridianul. 

Consecința imediată este că două astfel de „drepte” se intersectează, deci nu există paralele în geometria pe sferă. Pentru a justifica asta, cel mai ușor este să vă imaginați două meridiane (deci două „drepte” ale sferei). Ele se intersectează obligatoriu în N și S.  Deci orice două „drepte” pe sferă  se intersectează exact cum se intersectează cele două meridiane, deci nu există „drepte” care nu se intersectează. Deci nu există paralele. 

Această geometrie sferică este geometria naturală a boltei cerești, esențială în astronomie și indispensabilă navigatorilor din epocile pre-satelitare, când poziția pe glob se deducea doar din observația cerului și din calcule trigonometrice.

Primele mari teoreme ale geometriei sferice au fost deduse de Menelaus, Al-Jayyani, Jabir Ibn Aflah, și Girolamo Cardano, între secolul I și secolul al XV-lea al erei noastre. Deci au fost necesari 1500 de ani pentru geometria în sine și încă mai mult dacă vrem să o vedem înțeleasă prin limbajul geometriei diferențiale.

Dacă e să vorbim despre rolul acestor geometrii în fizică, lucrurile devin și mai clare:

• Geometria euclidiană a fost considerată de Newton și Kant drept geometria spațiului absolut, necesară pentru modelarea lumii în mecanica clasică.

• Geometria sferică este indispensabilă în astronomie și navigație.

• Iar despre geometria neeuclidiană, ne pregătim să vorbim mai pe larg.

V. Cazul modelelor geometriilor neeuclidiene: pseudosfera, semiplanul lui Poincaré și discul lui Poincaré. 

Vom înțelege acum modul în care Poincaré, pornind de la geometria pseudosferei, a pus bazele unei revoluții: o geometrie a curburii negative, a spațiului hiperbolic, a lumilor posibile.

Poincaré a imaginat două modele de geometrie neeuclidiană. Modelul discului și modelul semiplanului. 

Să încercăm să le explicăm cât mai simplu și să vedem cum se conectează ele cu pseudosfera.

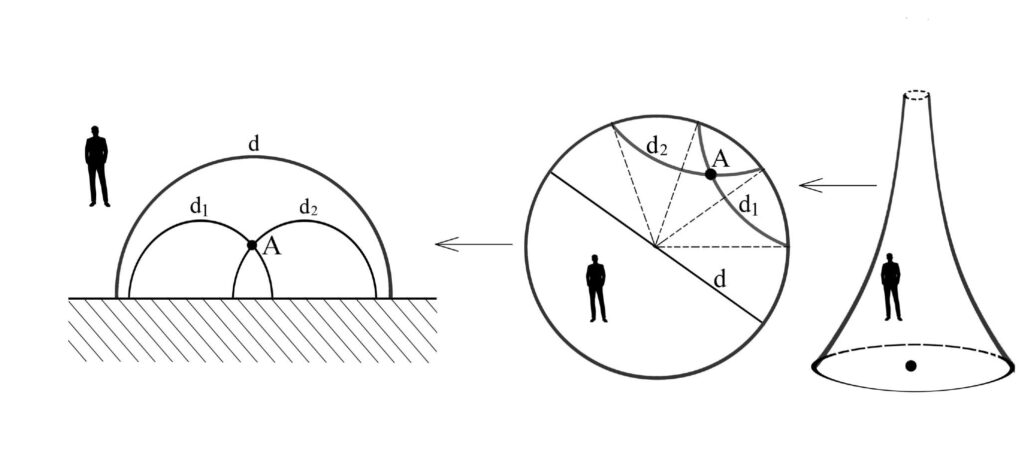
Mai întâi să arătăm că într-un semiplan al unui plan putem să construim un model de geometrie neeuclidiană. Cum facem? Considerăm dată o dreaptă d în plan. Alegem unul dintre cele două semiplane mărginite de dreapta d și îl vopsim în negru. Pentru noi acest semiplan nu mai există. 

În celălalt semiplan dezvoltăm geometria neeuclidiană spunând întâi cine sunt „dreptele” ei. Poincaré a considerat mai întâi toate cercurile care au centrul pe dreapta d și dreptele perpendiculare pe d. Referitor la cercurile care au centrul pe dreapta d: jumătate din cerc este în planul vopsit cu negru. Poincaré a considerat că semicercul din planul nevopsit este o „dreaptă” în noua geometrie. La fel pentru dreptele perpendiculare pe d. Partea din semiplanul vopsit cu negru nu interesează. Doar semidreapta rămasă în celălalt semiplan este „dreaptă” în noua geometrie. 

Mai putem să observăm că semicercurile intersectează dreapta d în unghiuri de 90° grade. Vom spune că sunt perpendiculare la dreapta d. 

Dacă iau două puncte A și B pe această „dreaptă”, drumul cel mai scurt pe care l-ar parcurge un omuleț bidimensional este chiar pe arcul AB. Nu segmentul Euclidian AB. Acela este mai lung. Asta face noua geometrie imaginată de Poincaré aici. 

Să analizăm problema paralelelor.

Fie două astfel de „drepte” care se intersectează în A. Să le numim a și b. Deci practic avem două semicercuri care se intersectează în A. Există un semicerc („dreaptă”) mai mare, f, care cuprinde in interiorul lui cele două semicercuri („drepte”) care se intersectează în A. Fiecare dintre ele, a și b, nu intersectează f. Deci am construit două paralele prin A la dreapta f. Practic se pot construi o infinitate de paralele. 

Se arată apoi (mai greu) că suma unghiurilor unui triunghi este mai mică strict decât 180°. 

Toate lucrurile spuse anterior au sens în spiritul geometriei diferențiale, varianta Bernhard Riemann, obiectele respective fiind geodezice pentru ceea ce se numește metrica lui Poincaré pentru semiplan. Deci nu mai pot fi explicate elevilor decât așa, la nivelul intuiției. Demonstrațiile țin de formalismul geometriei diferențiale. 

Acum intervine esențialul, transferul de structuri.

Poincaré a arătat că există o schimbare de coordonate care transformă metrica pseudosferei în metrica semiplanului său. Un transfer de structuri care arată că în ambele cazuri se evidențiază o aceiași geometrie, cea neeuclidiană, funcționând atât pe pseudosferă cât și în semiplan.

Iar ideea poate fi continuată. 

Printr-o inversiune geometrică convenabilă (nematematicienii citesc asta: printr-o transformare a planului convenabilă) semiplanul Poincaré se transformă într-un disc, adică în interiorul unui cerc. Deci înțelegeți cum funcționează transformarea? Dreapta d se transformă în cercul C, punctele din semiplan se transformă fiecare într-un punct al discului, „dreptele” semiplanului se transformă în „drepte” ale discului păstrând unghiurile. Astfel toți diametrii discului și toate arcele de cerc „dublu perpendiculare cercului” sunt „drepte” ale discului. Metrica semiplanului se transformă în metrica discului. Se poate arăta că toate metricile de care vorbim au curbură Gauss constantă negativă. 

Toate structurile acestea, pseudosferă, semiplan Poincaré și disc Poincaré sunt modele, imagini, pentru geometria neeuclidiană. 

VI. „Singurătatea Matematicianului” – ar exclama Solomon Marcus

Suntem în anul în care profesorul Solomon Marcus ar fi împlinit 100 de ani. Un veac de singurătate, dacă ar fi să considerăm eseul domniei sale despre matematicieni și singurătatea lor. Nu socială! Ci singurătatea lor în fața frumosului matematicii. Să îi aducem un omagiu explicând în câteva idei de ce frumusețea matematicii te poate face să te simți singur. Vom folosi ingredientele din acest episod.

Să considerăm un omuleț în centrul discului și să presupunem că el începe să se deplaseze pe o rază spre cercul care mărginește discul. Nu va ajunge niciodată acolo. Va fi ca o furnică care vrea să afle marginea unui plan mergând pe o dreaptă din plan. De ce? Geometria neeuclidiană vine împreună cu un alt mod de măsurare a distanțelor. Distanța Euclidiană care reprezintă mărimea razei, devine infinit – așa se schimbă structurile. 

Deci, dacă ne întoarcem la semiplanul Poincaré, distanța de la A la d este tot infinit. 

Dreapta d care mărginește semiplanul Poincaré și cercul C care mărginește discul lui Poincaré devin domenii ale infinitului geometriilor respective. 

Discul inițial, de rază finită în geometria Euclidiană, devine un spațiu neeuclidian infinit. Pentru asta nu aveți decât să acceptați că matematicienii au stabilit că x din intervalul (0,R) se transformă în log (R+x)/(R-x) . Când x tinde către lungimea R a razei, acel logaritm tinde către infinit. 

Aceasta este puterea matematicii și cumva este responsabilă pentru singurătatea matematicianului. 

Un matematician lucrează cu structuri extrem de abstracte care de multe ori nu au echivalent în realitate. Matematicienii le văd, le înțeleg, și le leagă între ele folosind limbajul matematic. Un formalism necesar pentru rigoare.

Dorința nematematicienilor de a înțelege structurile abstracte se poate lovi de formalismul matematic care le pare excesiv. 

Pe când mintea matematicianului, așa cum am spus, se poate juca ușor cu structuri care au aceeași semnificație dar arată diferit, pentru că formulele de transformare sunt singurele care-i dictează înțelesul corect. Și asta se întâmplă și în cazul schimbării obiectelor geometriilor neeuclidiene de mai sus. 

În episodul viitor vom arăta cum aceste exemple de geometrii neeuclidiene au influențat viziunea filozofică a lui Poincaré, transformându-l într-un adept al convenționalismului rațional și structural.